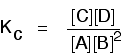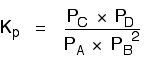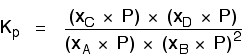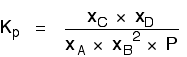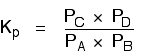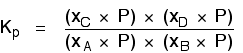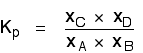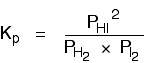|
EQUILIBRIUM CONSTANTS and LE CHATELIER'S PRINCIPLE This page looks at the relationship between equilibrium constants and Le Chatelier's Principle. Students often get confused about how it is possible for the position of equilibrium to change as you change the conditions of a reaction, although the equilibrium constant may remain the same. Be warned that this page assumes a good understanding of Le Chatelier's Principle and how to write expressions for equilibrium constants. | |||||||
|
Important: If you aren't happy about the basics of equilibrium, explore the equilibrium menu before you waste your time on this page. This page should only be read when you are confident about everything else to do with equilibria. | |||||||
|
Changing concentrations The facts Equilibrium constants aren't changed if you change the concentrations of things present in the equilibrium. The only thing that changes an equilibrium constant is a change of temperature. The position of equilibrium is changed if you change the concentration of something present in the mixture. According to Le Chatelier's Principle, the position of equilibrium moves in such a way as to tend to undo the change that you have made. Suppose you have an equilibrium established between four substances A, B, C and D.
According to Le Chatelier's Principle, if you decrease the concentration of C, for example, the position of equilibrium will move to the right to increase the concentration again. | |||||||
|
Note: The reason for choosing an equation with "2B" will become clearer when I deal with the effect of pressure further down the page. | |||||||
|
Explanation in terms of the constancy of the equilibrium constant The equilibrium constant, Kc for this reaction looks like this:
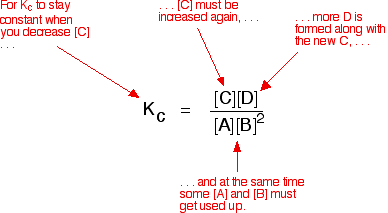
If you have moved the position of the equilibrium to the right (and so increased the amount of C and D), why hasn't the equilibrium constant increased? This is actually the wrong question to ask! We need to look at it the other way round. Let's assume that the equilibrium constant mustn't change if you decrease the concentration of C - because equilibrium constants are constant at constant temperature. Why does the position of equilibrium move as it does? If you decrease the concentration of C, the top of the Kc expression gets smaller. That would change the value of Kc. In order for that not to happen, the concentrations of C and D will have to increase again, and those of A and B must decrease. That happens until a new balance is reached when the value of the equilibrium constant expression reverts to what it was before. The position of equilibrium moves - not because Le Chatelier says it must - but because of the need to keep a constant value for the equilibrium constant. If you decrease the concentration of C:
Changing pressure This only applies to systems involving at least one gas. The facts Equilibrium constants aren't changed if you change the pressure of the system. The only thing that changes an equilibrium constant is a change of temperature. The position of equilibrium may be changed if you change the pressure. According to Le Chatelier's Principle, the position of equilibrium moves in such a way as to tend to undo the change that you have made. That means that if you increase the pressure, the position of equilibrium will move in such a way as to decrease the pressure again - if that is possible. It can do this by favouring the reaction which produces the fewer molecules. If there are the same number of molecules on each side of the equation, then a change of pressure makes no difference to the position of equilibrium. Explanation Where there are different numbers of molecules on each side of the equation Let's look at the same equilibrium we've used before. This one would be affected by pressure because there are 3 molecules on the left but only 2 on the right. An increase in pressure would move the position of equilibrium to the right.
Because this is an all-gas equilibriium, it is much easier to use Kp:
Once again, it is easy to suppose that, because the position of equilibrium will move to the right if you increase the pressure, Kp will increase as well. Not so! To understand why, you need to modify the Kp expression. Remember the relationship between partial pressure, mole fraction and total pressure?
| |||||||
|
Note: If you aren't happy with this, read the beginning of the page about Kp before you go on. Use the BACK button on your browser to return to this page. | |||||||
|
Replacing all the partial pressure terms by mole fractions and total pressure gives you this:
If you sort this out, most of the "P"s cancel out - but one is left at the bottom of the expression.
Now, remember that Kp has got to stay constant because the temperature is unchanged. How can that happen if you increase P? To compensate, you would have to increase the terms on the top, xC and xD, and decrease the terms on the bottom, xA and xB. Increasing the terms on the top means that you have increased the mole fractions of the molecules on the right-hand side. Decreasing the terms on the bottom means that you have decreased the mole fractions of the molecules on the left. That is another way of saying that the position of equilibrium has moved to the right - exactly what Le Chatelier's Principle predicts. The position of equilibrium moves so that the value of Kp is kept constant. Where there are the same numbers of molecules on each side of the equation In this case, the position of equilibrium isn't affected by a change of pressure. Why not?
Let's go through the same process as before:
Substituting mole fractions and total pressure:
. . . and cancelling out as far as possible:
There isn't a single "P" left in the expression. Changing the pressure can't make any difference to the Kp expression. The position of equilibrium doesn't need to move to keep Kp constant. Changing temperature The facts Equilibrium constants are changed if you change the temperature of the system. Kc or Kp are constant at constant temperature, but they vary as the temperature changes. Look at the equilibrium involving hydrogen, iodine and hydrogen iodide:
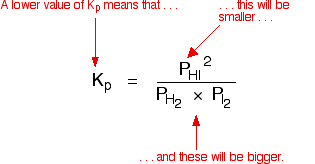
The Kp expression is:
Two values for Kp are:
You can see that as the temperature increases, the value of Kp falls. | |||||||
|
Note: You might possibly be wondering what the units of Kp are. This particular example was chosen because in this case, Kp doesn't have any units. It is just a number. The units for equilibrium constants vary from case to case. It is much easier to understand this from a book than from a lot of maths on screen. You will find this explained in my chemistry calculations book. | |||||||
|
This is typical of what happens with any equilibrium where the forward reaction is exothermic. Increasing the temperature decreases the value of the equilibrium constant. Where the forward reaction is endothermic, increasing the temperature increases the value of the equilibrium constant. | |||||||
|
Note: Any explanation for this needs knowledge beyond the scope of any UK A level (or equivalent) syllabus. | |||||||
|
The position of equilibrium also changes if you change the temperature. According to Le Chatelier's Principle, the position of equilibrium moves in such a way as to tend to undo the change that you have made. If you increase the temperature, the position of equilibrium will move in such a way as to reduce the temperature again. It will do that by favouring the reaction which absorbs heat. In the equilibrium we've just looked at, that will be the back reaction because the forward reaction is exothermic.
So, according to Le Chatelier's Principle the position of equilibrium will move to the left. Less hydrogen iodide will be formed, and the equilibrium mixture will contain more unreacted hydrogen and iodine. That is entirely consistent with a fall in the value of the equilibrium constant.
Adding a catalyst The facts Equilibrium constants aren't changed if you add (or change) a catalyst. The only thing that changes an equilibrium constant is a change of temperature. The position of equilibrium is not changed if you add (or change) a catalyst. Explanation A catalyst speeds up both the forward and back reactions by exactly the same amount. Dynamic equilibrium is established when the rates of the forward and back reactions become equal. If a catalyst speeds up both reactions to the same extent, then they will remain equal without any need for a shift in position of equilibrium. | |||||||
|
Note: If you know about the Arrhenius equation, it isn't too difficult to use it to show that the ratio of the rate constants for the forward and back reactions isn't affected by adding a catalyst. Although the activation energies for the two reactions change when you add a catalyst, they both change by the same amount.
I'm not going to do this bit of algebra, because it would never be asked at this level (UK A level or equivalent). | |||||||
© Jim Clark 2002 (last modified March 2021) |
|||||||