|
Other gas laws - Boyle's Law and Charles' Law This page takes a simple look at Boyle's Law and Charles' Law, and is suitable for 16 - 18 year old chemistry students doing a course the equivalent of UK A level. The aim is simply to show how these laws relate to Kinetic Theory (in a non-mathematical way), and to the ideal gas equation. Before you waste time on this, be sure that you actually need to know about it. Certainly in the UK exam system, it is pretty rare for chemistry students to be expected to know either of these laws these days. They have been almost completely replaced by the ideal gas equation. Boyle's Law Statement
Is this consistent with pV = nRT ?
That means that everything on the right-hand side of pV = nRT is constant, and so pV is constant - which is what we have just said is a result of Boyle's Law. Simple Kinetic Theory explanation I'm not going to try to prove the relationship between pressure and volume mathematically - I'm just showing that it is reasonable. This is easiest to see if you think about the effect of decreasing the volume of a fixed mass of gas at constant temperature. Pressure is caused by gas molecules hitting the walls of the container. With a smaller volume, the gas molecules will hit the walls more frequently, and so the pressure increases. You might argue that this isn't actually what Boyle's Law says - it wants you to increase the pressure first and see what effect that has on the volume. But, in fact, it amounts to the same thing. If you want to increase the pressure of a fixed mass of gas without changing the temperature, the only way you can do it is to squeeze it into a smaller volume. That causes the molecules to hit the walls more often, and so the pressure increases. Charles' Law Statement
That means, for example, that if you double the kelvin temperature from, say to 300 K to 600 K, at constant pressure, the volume of a fixed mass of the gas will double as well.
Is this consistent with pV = nRT ?
If you rearrange the pV = nRT equation by dividing both sides by p, you will get
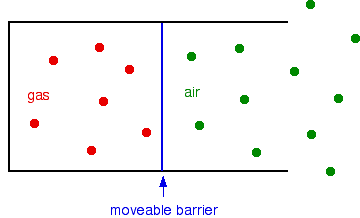
But everything in the nR/p part of this is constant. That means that V = constant x T, which is Charles' Law. Simple Kinetic Theory explanation Again, I'm not trying to prove the relationship between pressure and volume mathematically - just that it is reasonable. Suppose you have a fixed mass of gas in a container with a moveable barrier - something like a gas syringe, for example. The barrier can move without any sort of resistance.
The barrier will settle so that the pressure inside and outside is identical. Now suppose you heat the gas, but not the air outside. The gas molecules will now be moving faster, and so will hit the barrier more frequently, and harder. Meanwhile, the air molecules on the outside are hitting it exactly as before. Obviously, the barrier will be forced to the right, and the volume of the gas will increase. That will go on until the pressure inside and outside is the same. In other words, the pressure of the gas will be back to the same as the air again. So we have fulfilled what Charles' Law says. We have a fixed mass of gas (nothing has been added, and nothing has escaped). The pressure is the same before and after (in each case, the same as the external air pressure). And the volume increases when you increase the temperature of the gas. What we haven't shown, of course, is that there is a "directly proportional" relationship. It can be done, but it needs some maths.
To the kinetic theory menu . . . © Jim Clark 2010 (modified October 2013) |
||