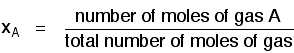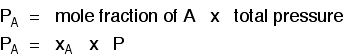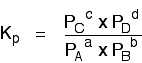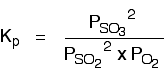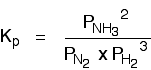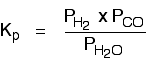|
EQUILIBRIUM CONSTANTS: Kp This page explains equilibrium constants expressed in terms of partial pressures of gases, Kp. It covers an explanation of the terms mole fraction and partial pressure, and looks at Kp for both homogeneous and heterogeneous reactions involving gases. The page assumes that you are already familiar with the concept of an equilibrium constant, and that you know about Kc - an equilibrium constant expressed in terms of concentrations | |||||||||||||
|
Important: If you have come directly to this page via a search engine, you should first read the page on equilibrium constants - Kc before you go on - unless you are already fully confident about how to write expressions for Kc. You will find a link back to this page at the bottom of the Kc page. | |||||||||||||
|
Defining some terms Before we can go any further, there are two terms relating to mixtures of gases that you need to be familiar with. Mole fraction If you have a mixture of gases (A, B, C, etc), then the mole fraction of gas A is worked out by dividing the number of moles of A by the total number of moles of gas. The mole fraction of gas A is often given the symbol xA. The mole fraction of gas B would be xB - and so on.
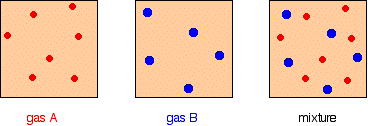
Pretty obvious really! For example, in a mixture of 1 mole of nitrogen and 3 moles of hydrogen, there are a total of 4 moles of gas. The mole fraction of nitrogen is 1/4 (0.25) and of hydrogen is 3/4 (0.75). Partial pressure The partial pressure of one of the gases in a mixture is the pressure which it would exert if it alone occupied the whole container. The partial pressure of gas A is often given the symbol PA. The partial pressure of gas B would be PB - and so on. There are two important relationships involving partial pressures. The first is again fairly obvious. The total pressure of a mixture of gases is equal to the sum of the partial pressures.
It is easy to see this visually:
Gas A is creating a pressure (its partial pressure) when its molecules hit the walls of its container. Gas B does the same. When you mix them up, they just go on doing what they were doing before. The total pressure is due to both molecules hitting the walls - in other words, the sum of the partial pressures. The more important relationship is the second one:
Learn it! That means that if you had a mixture made up of 20 moles of nitrogen, 60 moles of hydrogen and 20 moles of ammonia (a total of 100 moles of gases) at 200 atmospheres pressure, the partial pressures would be calculated like this:
Partial pressures can be quoted in any normal pressure units. The common ones are atmospheres or pascals (Pa). Pascals are exactly the same as N m-2 (newtons per square metre). Kp in homogeneous gaseous equilibria A homogeneous equilibrium is one in which everything in the equilibrium mixture is present in the same phase. In this case, to use Kp, everything must be a gas. A good example of a gaseous homogeneous equilibrium is the conversion of sulphur dioxide to sulphur trioxide at the heart of the Contact Process:
Writing an expression for Kp We are going to start by looking at a general case with the equation:
If you allow this reaction to reach equilibrium and then measure (or work out) the equilibrium partial pressures of everything, you can combine these into the equilibrium constant, Kp. Just like Kc, Kp always has the same value (provided you don't change the temperature), irrespective of the amounts of A, B, C and D you started with.
Kp has exactly the same format as Kc, except that partial pressures are used instead of concentrations. The gases on the right-hand side of the chemical equation are at the top of the expression, and those on the left at the bottom. | |||||||||||||
|
Beware! People are sometimes tempted to write brackets around the individual partial pressure terms. Don't do it! Even if you intend to write normal round brackets, it is too easy in an exam to write them as square brackets instead. This makes it look as if you are confusing Kp with Kc. Examiners don't like it, and you could be penalised. | |||||||||||||
|
The Contact Process equilibrium You will remember that the equation for this is:
Kp is given by:
The Haber Process equilibrium The equation for this is:
. . . and the Kp expression is:
Kp in heterogeneous equilibria A typical example of a heterogeneous equilibrium will involve gases in contact with solids. Writing an expression for Kp for a heterogeneous equilibrium Exactly as happens with Kc, you don't include any term for a solid in the equilibrium expression. The next two examples have already appeared on the Kc page. The equilibrium produced on heating carbon with steam
Everything is exactly the same as before in the expression for Kp, except that you leave out the solid carbon.
The equilibrium produced on heating calcium carbonate This equilibrium is only established if the calcium carbonate is heated in a closed system, preventing the carbon dioxide from escaping.
The only thing in this equilibrium which isn't a solid is the carbon dioxide. That is all that is left in the equilibrium constant expression.
Calculations involving Kp On the Kc page, I've already discussed the fact that the internet isn't a good medium for learning how to do calculations. If you want lots of worked examples and problems to do yourself centred around Kp, you might be interested in my book on chemistry calculations. | |||||||||||||
|
Note: If you are interested in my chemistry calculations book you might like to follow this link. | |||||||||||||
© Jim Clark 2002 (modified May 2013) |
|||||||||||||