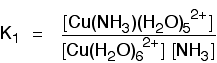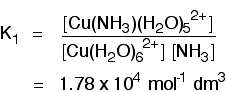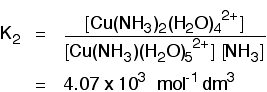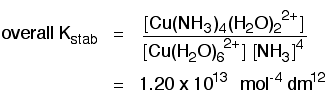|
COMPLEX METAL IONS - STABILITY CONSTANTS This page explains what is meant by a stability constant for a complex ion, and goes on to look at how its size is governed in part by the entropy change during a ligand exchange reaction. | |||||||||||||||||||||
|
Note: If you aren't happy about what a ligand exchange reaction is, it would be useful to have a quick look at this link before you go on. There is no need to worry about the detail, but you should read enough to get a feel for what we are talking about. | |||||||||||||||||||||
|
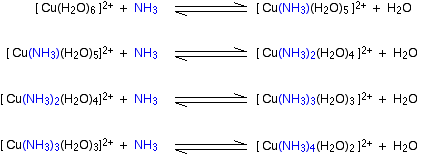
What is a stability constant? Replacing water by ammonia around copper(II) ions If you add ammonia solution to a solution containing hexaaquacopper(II) ions, [Cu(H2O)6]2+, four of the water molecules are eventually replaced by ammonia molecules to give [Cu(NH3)4(H2O)2]2+. This can be written as an equilibrium reaction to show the overall effect:
In fact, the water molecules get replaced one at a time, and so this is made up of a series of part-reactions:
Although this can look a bit daunting at first sight, all that is happening is that first you have one, then two, then three, then four water molecules in total replaced by ammonias. Individual stability constants Let's take a closer look at the first of these equilibria:
Like any other equilibrium, this one has an equilibrium constant, Kc - except that in this case, we call it a stability constant. Because this is the first water molecule to be replaced, we call it K1. | |||||||||||||||||||||
|
Warning! If you aren't happy about how to write expressions for equilibrium constants, it is essential to follow this link before you go any further. Use the BACK button on your browser to return quickly to this page. | |||||||||||||||||||||
|
Here is the equation again:
K1 is given by this expression:
There are two points of possible confusion here - one minor, one more important!
With that out of the way, let's go back to where we were - but introduce a value for K1:
The value of the equilibrium constant is fairly large, suggesting that there is a strong tendency to form the ion containing an ammonia molecule. A high value of a stability constant shows that the ion is easily formed. Each of the other equilibria above also has its own stability constant, K2, K3 and K4. For example, K2 is given by:
The ion with two ammonias is even more stable than the ion with one ammonia. You could keep plugging away at this and come up with the following table of stability constants:
You will often find these values quoted as log K1 or whatever. All this does is tidy the numbers up so that you can see the patterns more easily. The ions keep on getting more stable as you replace up to 4 water molecules, but notice that the equilibrium constants are gradually getting less big as you replace more and more waters. This is common with individual stability constants. Overall stability constants The overall stability constant is simply the equilibrium constant for the total reaction:
It is given by this expression:
You can see that overall this is a very large equilibrium constant, implying a high tendency for the ammonias to replace the waters. The "log" value is 13.1. This overall value is found by multiplying together all the individual values of K1, K2 and so on. To find out why that works, you will need a big bit of paper and some patience! Write down expressions for all the individual values (the first two are done for you above), and then multiply those expressions together. You will find that all the terms for the intermediate ions cancel out to leave you with the expression for the overall stability constant. Summary Whether you are looking at the replacement of individual water molecules or an overall reaction producing the final complex ion, a stability constant is simply the equilibrium constant for the reaction you are looking at. The larger the value of the stability constant, the further the reaction lies to the right. That implies that complex ions with large stability constants are more stable than ones with smaller ones. Stability constants tend to be very large numbers. In order to simplify the numbers a "log" scale is often used. Because of the way this works, a difference of 1 in the log value comes from a 10 times difference in the stability constant. A difference of 2 comes from a 100 (in other words, 102) times difference in stability constant - and so on. Stability constants and entropy - the chelate effect What is the chelate effect? This is an effect which happens when you replace water (or other simple ligands) around the central metal ion by multidentate ligands like 1,2-diaminoethane (often abbreviated to "en") or EDTA. | |||||||||||||||||||||
|
Important! If words like multidentate ligand or EDTA don't mean anything to you, then it is essential that you read the introductory page on complex ions. The second half of that page deals with multidentate ligands. Use the BACK button on your browser to return quickly to this page. | |||||||||||||||||||||
|
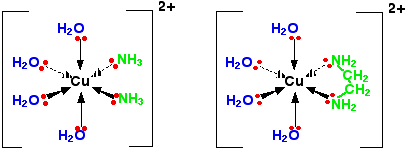
Compare what happens if you replace two water molecules around a [Cu(H2O)6]2+ ion with either 2 ammonia molecules or one molecule of 1,2-diaminoethane.
This second structure is known as a chelate from a Greek word meaning a crab's claw. You can picture the copper ion as being nipped by the claw of the 1,2-diaminoethane molecule. Chelates are much more stable than complex ions formed from simple monodentate ligands. The overall stability constants for the two ions are:
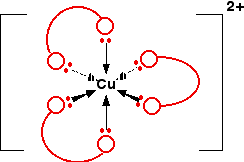
The reaction with the 1,2-diaminoethane could eventually go on to produce a complex ion [Cu(en)3]2+. Simplifying the structure of this:
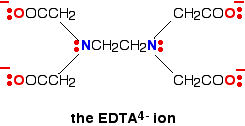
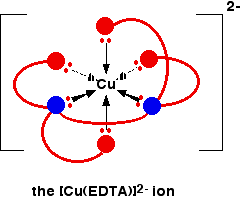
The overall stability constant for this (as log K) is 18.7. Another copper-based chelate comes from the reaction with EDTA.
This also has a high stability constant - log K is 18.8. However many examples you take, you always find that a chelate (a complex ion involving multidentate ligands) is more stable than ions with only unidentate ligands. This is known as the chelate effect. The reason for the chelate effect If you compare the two equilibria below, the one with the 1,2-diaminoethane ("en") has the higher equilibrium (stability) constant (for values, see above).
The enthalpy changes of the two reactions are fairly similar. You might expect this because in each case you are breaking two bonds between copper and oxygen atoms and replacing them by two bonds between copper and nitrogen atoms. | |||||||||||||||||||||
|
Note: This is an over-simplification. You have to consider interactions between the various species and water molecules (from the solvent) as well. | |||||||||||||||||||||
|
If the enthalpy changes are similar, what causes the difference in the extent to which the two reactions happen? You need to think about the entropy change during each reaction. Entropy is most easily thought of as a measure of disorder. Any change which increases the amount of disorder increases the tendency of a reaction to happen. | |||||||||||||||||||||
|
Note: If you want a more formal approach to entropy, I'm afraid you will have to look elsewhere. You will find a gentle introduction to the mathematical side of entropy in my chemistry calculations book. | |||||||||||||||||||||
|
If you look again at the two equililbria, you might notice that the 1,2-diaminoethane equilibrium does lead to an increase in the disorder of the system (an increase in its entropy). There are only two species on the left-hand side of the equation, but three on the right.
You can obviously get more disorder out of three species than out of only two. Compare that with the other equilibrium. In this case, there is no change in the total number of species before and after reaction, and so no useful contribution to an increase in entropy.
In the case of the complex with EDTA, the increase in entropy is very pronounced.
Here, we are increasing the number of species present from two on the left-hand side to seven on the right. You can get a major amount of increase in disorder by making this change. Reversing this last change is going to be far more difficult in entropy terms. You would have to move from a highly disordered state to a much more ordered one. That isn't so likely to happen, and so the copper-EDTA complex is very stable. Summary Complexes involving multidentate ligands are more stable than those with only unidentate ligands in them. The underlying reason for this is that each multidentate ligand displaces more than one water molecule. This leads to an increase in the number of species present in the system, and therefore an increase in entropy. An increase in entropy makes the formation of the chelated complex more favourable.
© Jim Clark 2003 (last modified January 2015) |
|||||||||||||||||||||